First of all - Happy New Year of 2019 to all! 👑🎉🎊
To kick off the year with a big bang, let’s start with today’s post.
From my previous post little over ago or so, I discussed the importance of knowing data structures such as arrays, stacks, queues etc every good software developer/engineer must grasp. In this post, I will be covering topics on the other not-so-common data structures that we normally (or always, should I say) use when implementing our algorithms.
They are follows:
- Trees
- Graphs
- Heaps
- Trie
##Data Structures
###a) Trees
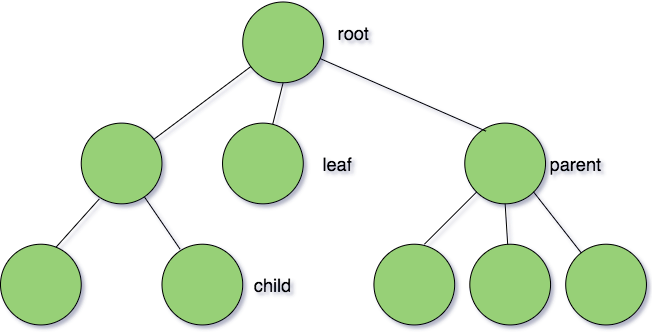
A binary tree is a tree whose elements have at most 2 children. Each element in a binary tree can have only 2 children thus we typically name them left and right nodes respectively. Typically a tree node has the following properties
- Data
- Left Pointer
- Right Pointer
The top most node in the tree is called the root. Every node (except the root node) in a tree is connected by a directed edge from exactly one node to another. This node is called the parent node. Sometimes, a node can have more than 2 connected nodes to itself. Nodes with no children are called leaves or external nodes. Nodes which are not leaves are called internal nodes.
Next, we have a special kind of binary tree called the Binary Search Tree (BST). This tree is mainly used for storing repository that offers efficient ways of sorting, searching and retrieving data.
A BST is a binary tree where nodes are ordered in the following way:
- each node contains a key (or data)
- the keys in the left subtree are less than the key in its parent node.
- the keys in the right subtree are greater than the key in its parent node.
- duplicate keys are not allowed.
Finally, we have a binary tree traversal which is a process that visits all the nodes in the trees. When traversing trees, we consider a couple of traversal search approaches for doing such exercise.
- Depth First Search
- Breath First Search
Using depth first search approach, we have the following types of traversals to pick on:
- Preorder traversal - visit parent first, then left and right children.
- Inorder traversal - visit the left first, then parent and right child.
- Postorder traversal - visit the left first, then right child and parent.
With breadth-first search, there’s one type of traversal method which is level order traversal. This type of traversal visits nodes by levels from top to bottom and from left to right.
Binary Trees and Binary Search Trees .
Binary Tree Traversal.
All popular programming languages I know or aware of supports them - such as the following.
####Java
import java.util.*;
public class BinaryTree {
Node root;
public void add(int value) {
root = addRecursive(root, value);
}
private Node addRecursive(Node current, int value) {
if (current == null) {
return new Node(value);
}
if (value < current.value) {
current.left = addRecursive(current.left, value);
} else if (value > current.value) {
current.right = addRecursive(current.right, value);
}
return current;
}
public boolean isEmpty() {
return root == null;
}
public int getSize() {
return getSizeRecursive(root);
}
private int getSizeRecursive(Node current) {
return current == null ? 0 : getSizeRecursive(current.left) + 1 + getSizeRecursive(current.right);
}
public boolean containsNode(int value) {
return containsNodeRecursive(root, value);
}
private boolean containsNodeRecursive(Node current, int value) {
if (current == null) {
return false;
}
if (value == current.value) {
return true;
}
return value < current.value
? containsNodeRecursive(current.left, value)
: containsNodeRecursive(current.right, value);
}
public void delete(int value) {
root = deleteRecursive(root, value);
}
private Node deleteRecursive(Node current, int value) {
if (current == null) {
return null;
}
if (value == current.value) {
// Case 1: no children
if (current.left == null && current.right == null) {
return null;
}
// Case 2: only 1 child
if (current.right == null) {
return current.left;
}
if (current.left == null) {
return current.right;
}
// Case 3: 2 children
int smallestValue = findSmallestValue(current.right);
current.value = smallestValue;
current.right = deleteRecursive(current.right, smallestValue);
return current;
}
if (value < current.value) {
current.left = deleteRecursive(current.left, value);
return current;
}
current.right = deleteRecursive(current.right, value);
return current;
}
private int findSmallestValue(Node root) {
return root.left == null ? root.value : findSmallestValue(root.left);
}
public void traverseInOrder(Node node) {
if (node != null) {
traverseInOrder(node.left);
System.out.print(" " + node.value);
traverseInOrder(node.right);
}
}
public void traversePreOrder(Node node) {
if (node != null) {
System.out.print(" " + node.value);
traversePreOrder(node.left);
traversePreOrder(node.right);
}
}
public void traversePostOrder(Node node) {
if (node != null) {
traversePostOrder(node.left);
traversePostOrder(node.right);
System.out.print(" " + node.value);
}
}
public void traverseLevelOrder() {
if (root == null) {
return;
}
Queue<Node> nodes = new LinkedList<>();
nodes.add(root);
while (!nodes.isEmpty()) {
Node node = nodes.remove();
System.out.print(" " + node.value);
if (node.left != null) {
nodes.add(node.left);
}
if (node.left != null) {
nodes.add(node.right);
}
}
}
class Node {
int value;
Node left;
Node right;
Node(int value) {
this.value = value;
right = null;
left = null;
}
}
}####Python
#!/usr/bin/python
class Node:
def __init__(self,info):
self.info = info
self.left = None
self.right = None
self.level = None
def __str__(self):
return str(self.info)
class BinarySearchTree:
def __init__(self): #constructor of class
self.root = None
def create(self,val): #create binary search tree nodes
if self.root == None:
self.root = Node(val)
else:
current = self.root
while 1:
if val < current.info:
if current.left:
current = current.left
else:
current.left = Node(val)
break;
elif val > current.info:
if current.right:
current = current.right
else:
current.right = Node(val)
break;
else:
break
def inorder(self,node):
if node is not None:
self.inorder(node.left)
print node.info
self.inorder(node.right)
def preorder(self,node):
if node is not None:
print node.info
self.preorder(node.left)
self.preorder(node.right)
def postorder(self,node):
if node is not None:
self.postorder(node.left)
self.postorder(node.right)
print node.info####Ruby
#!/usr/bin/ruby
class BinarySearchTree
class Node
attr_reader :key, :left, :right
def initialize( key )
@key = key
@left = nil
@right = nil
end
def insert( new_key )
if new_key <= @key
@left.nil? ? @left = Node.new( new_key ) : @left.insert( new_key )
elsif new_key > @key
@right.nil? ? @right = Node.new( new_key ) : @right.insert( new_key )
end
end
end
def initialize
@root = nil
end
def insert( key )
if @root.nil?
@root = Node.new( key )
else
@root.insert( key )
end
end
def in_order(node=@root, &block)
return if node.nil?
in_order(node.left, &block)
yield node
in_order(node.right, &block)
end
def pre_order(node=@root, &block)
return if node.nil?
yield node
pre_order(node.left, &block)
pre_order(node.right, &block)
end
def post_order(node=@root, &block)
return if node.nil?
post_order(node.left, &block)
post_order(node.right, &block)
yield node
end
def search( key, node=@root )
return nil if node.nil?
if key < node.key
search( key, node.left )
elsif key > node.key
search( key, node.right )
else
return node
end
end
def check_height(node)
return 0 if node.nil?
leftHeight = check_height(node.left)
return -1 if leftHeight == -1
rightHeight = check_height(node.right)
return -1 if rightHeight == -1
diff = leftHeight - rightHeight
if diff.abs > 1
-1
else
[leftHeight, rightHeight].max + 1
end
end
def is_balanced?(node=@root)
check_height(node) == -1 ? false : true
end
end####Javascript
class Node {
constructor(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
insert(new_data) {
if new_data <= this.data {
if (this.left == null ?) {
this.left = new Node( new_data )
}
else {
this.left.insert( new_data )
}
}
else if (new_data > this.data) {
if(this.right == null) {
this.right = new Node( new_data )
}
else{
this.right.insert( new_data )
}
}
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insertNode(new_data) {
if (this.root == null) {
this.root = new Node(new_data)
}
else {
this.root.insert(new_data)
}
}
inOrderTraversal(node) {
if(node == null) {
return
}
in_order(node.left)
console.log(node)
in_order(node.right)
}
preOrderTraversal(node) {
if(node == null) {
return
}
console.log(node)
inOrderTraversal(node.left)
inOrderTraversal(node.right)
}
postOrderTraversal(node) {
if(node == null) {
return
}
inOrderTraversal(node.left, &block)
inOrderTraversal(node.right, &block)
console.log(node)
}
search(data, node ) {
if(node == null) {
return null;
}
if (data < node.data) {
search(data, node.left)
} else if(data > node.data) {
search(key, node.right)
} else {
return node;
}
}
checkHeight(node) {
if(node == null) {
return 0;
}
leftHeight = checkHeight(node.left)
if (leftHeight === -1) {
return -1;
}
rightHeight = checkHeight(node.right)
if (rightHeight === -1) {
return -1;
}
diff = leftHeight - rightHeight
if Math.abs(diff) > 1
return -1
else
return Math.max(leftHeight, rightHeight) + 1
end
}
isBalanced(node){
return (checkHeight(node) === -1) ? false : true
}
}####C++
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *left, *right;
};
struct node *newNode(int data) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void inorder(struct node *root) {
if(root != NULL) {
inorder(root->left);
printf(“%d \n”, root->key);
inorder(root->right);
}
}
void preorder(struct node *root) {
if(root != NULL) {
printf(“%d \n”, root->key);
preorder(root->left);
preorder(root->right);
}
}
void postorder(struct node *root) {
if(root != NULL) {
postorder(root->left);
postorder(root->right);
printf(“%d \n”, root->key);
}
}
struct node* insert(struct node* new_node, int new_data) {
if(new_node == NULL) return newNode(new_data);
if(new_data < new_node->key)
new_node-> left = insert(new_node->left, new_data);
else if(new_data > new_node->key)
new_node->right = insert(new_node->right, new_data)
return new_node;
}
int getHeight(struct node *current_node) {
if(current_node) return 0;
return 1 + max(getHeight(current_node->left), getHeight(current_node->right));
}
bool isBalanced(struct node *current_node) {
if(!current_node){
return false;
}
int leftHeight = getHeight(current_node->left);
int rightHeight = getHeight(current_node->right);
if (abs(leftHeight - rightHeight) > 1)
return
}####PHP
<?php
class Node {
public $info;
public $left;
public $right;
public $level;
public function __construct($info) {
$this->info = $info;
$this->left = NULL;
$this->right = NULL;
$this->level = NULL;
}
public function __toString() {
return "$this->info";
}
}
class SearchBinaryTree {
public $root;
public function __construct() {
$this->root = NULL;
}
public function create($info) {
if($this->root == NULL) {
$this->root = new Node($info);
} else {
$current = $this->root;
while(true) {
if($info < $current->info) {
if($current->left) {
$current = $current->left;
} else {
$current->left = new Node($info);
break;
}
} else if($info > $current->info){
if($current->right) {
$current = $current->right;
} else {
$current->right = new Node($info);
break;
}
} else {
break;
}
}
}
}
public function traverse($method) {
switch($method) {
case 'inorder':
$this->_inorder($this->root);
break;
case 'postorder':
$this->_postorder($this->root);
break;
case 'preorder':
$this->_preorder($this->root);
break;
default:
break;
}
}
private function _inorder($node) {
if($node->left) {
$this->_inorder($node->left);
}
echo $node. " ";
if($node->right) {
$this->_inorder($node->right);
}
}
private function _preorder($node) {
echo $node. " ";
if($node->left) {
$this->_preorder($node->left);
}
if($node->right) {
$this->_preorder($node->right);
}
}
private function _postorder($node) {
if($node->left) {
$this->_postorder($node->left);
}
if($node->right) {
$this->_postorder($node->right);
}
echo $node. " ";
}
}###b) Graphs
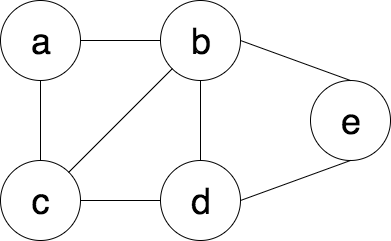
Next, we have a graphs.
Like trees, a graph is a non-linear data structure that consist of nodes and edges. The nodes are sometimes called vertices and edges are called lines or arcs for there may be more than two nodes connected to each other in the graph.
Graphs are used to solve many real-life problems. Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like LinkeIn, Facebook,
####Java
import java.util.*;
public class Vertex{
private int label;
Vertex(String label) {
this.label = label;
}
//equals and hashCode
@Override
public boolean equals(Object obj) {
if(this == obj) return true;
if(! (obj instanceof Vertext)) return false;
Vertex _obj = (Vertex) obj;
return _obj.label = this.label;
}
@Override
public int hashCode() {
return label;
}
@Override
public int getLabel(){
return label;
}
@Override
public void setLabel(int newValue){
this.label = newValue;
}
}
public class Graph {
private Map<Vertex, List<Vertex>> adjVertices;
public Graph() {
adjVertices = new Map<>()
}
public void addVertex(int label) {
adjVertices.add(new Vertex(label), new ArrayList<>());
}
public void removeVertex(int label) {
Vertex v = new Vertex(label);
adjVertices.values()
.stream()
.map(e -> e.remove(v))
.collect(Collectors.toList());
adjVertices.remove(new Vertex(label));
}
public void addEdge(int label1, int label2 ){
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
adjVertices.get(v1).add(v2);
adjVertices.get(v2).add(v1);
}
public void removeEdge(int label1, int label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
List<Vertex> eV1 = adjVertices.get(v1);
List<Vertex> eV1 = adjVertices.get(v1);
if (eV1 != null)
eV1.remove(v2);
if (eV2 != null)
eV2.remove(v1);
}
public List<Vertex> getAdjVertices(int label) {
return adjVertices.get(new Vertex(label));
}
}####Python
#!/usr/bin/python
class Vertex:
def __init___(self, label):
self.label = label
def equals(self):
return self.data
def hash_code(self):
return self.data
def get_label(self):
return self.data
def set_label(self, new_label):
self.label = new_label
class Graph:
def __init__(self, adj_vertices):
if adj_vertices == None:
adj_vertices = {}
self.adj_vertices = adj_vertices
def add_vertex(self, label):
vertex = Vertex(label)
if vertex not in self.adj_vertices:
self.adj_vertices[vertex] = []
def remove_vertex(self, label):
vertex = Vertex(label)
if vertex in self.adj_vertices:
del self.adj_vertices[vertex]
def add_edge(self, edge):
edge = set(edge)
(vertex1, vertex2) = tuple(edge)
if vertex1 in self.adj_vertices:
self.adj_vertices[vertex1].append(vertex2)
else:
self.adj_vertices[vertex1] = [vertex2]
def remove_edge(self, edge):
edge = set(edge)
(vertex1, vertex2) = tuple(edge)
if vertex1 in self.adj_vertices:
del self.adj_vertices[vertex1]
if vertex2 in self.adj_vertices:
del self.adj_vertices[vertex2]
def vertices(self):
return list(self.adj_vertices.keys())####Ruby
#!/usr/bin/ruby
class Vertex
attr_accessor :label
def initialise(label)
@label = label
end
def hash_code
@label
end
end
class Graph
attr_accessor :adj_vertices
def initialize()
@adj_vertices = []
end
def add_vertex(label)
@adj_vertices << Vertex.new(label)
end
def remove_vertex(label)
vertex = Vertex.new(label)
if @adj_vertices.include? vertex
@adj_vertices.delete(vertex)
end
end
def add_edge(label1, label2)
vertex1 = @adj_vertices.index { |v| v.label == label1}
vertex2 = @adj_vertices.index { |v| v.label == label2}
if @adj_vertices.include? @vertex1
@adj_vertices[@vertex1] << vertex2
else
@adj_vertices[@vertex1] = [vertex2]
end
end
def remove_edge(label1, label2)
vertex1 = @adj_vertices.index { |v| v.label == label1}
vertex2 = @adj_vertices.index { |v| v.label == label2}
if @adj_vertices.include? @vertex1
@adj_vertices.delete(vertex1)
end
if @adj_vertices.include? @vertex2
@adj_vertices.delete(vertex2)
end
end
def vertices
@vertices.length
end
end####Javascript
class Vertex {
constructor(label) {
this.label = label;
this.edges = {};
}
hasCode() {
return this.label;
}
}
class Graph {
constructor(adjVertices) {
this.adjVertices = adjVertices;
}
addVertex(label) {
if(!this.adjVertices[label]) {
this.adjVertices[label] = new Vertex(label);
}
}
removeVertex(label) {
if(this.adjVertices[label]) {
delete this.adjVertices[val];
Object.keys(this.adjVertices).forEach( (key, index) => {
if(this.adjVertices[key].edges[label] ){
delete this.adjVertices[key].edges[val];
}
}).bind(this);
}
}
addEdge(from, to) {
if(this.adjVertices[from] && this.adjVertices[to]) {
if(this.adjVertices[from].edges[to]) {
this.adjVertices[from].edges[to].weight +=1;
} else {
this.adjVertices[from].edges[to] = {weight: 1}
}
}
}
removeEdge(from, to) {
if(this.adjVertices[from] && this.adjVertices[to]){
if(this.adjVertices[from].edges[to]) {
delete this.adjVertices[from].edges[to];
}
}
}
getTotalVertices(label) {
return this.adjVertices[label];
}
};
####C++
#include <iostream>
using namespace std;
struct Vertex {
int label;
Vertex* next;
};
struct Edge {
int from, to;
}
class Graph {
Vertex* getAdjListNode(int to, Vertex* head) {
Vertex* newVertex = new Vertex;
newVertex->label = to;
newVertex->next = head;
return newVertex;
}
int N;
}
public:
Vertex **head;
Graph(Edge edges[], int n, int N)
{
head = new Vertex*[N]();
this->N = N;
for(int i = 0; i < N; i++)
head[i] = nullptr;
for(unsigned i = 0; i < n; i++)
{
int from = edges[i].src;
int dest = edges[i].dest;
Vertex* newVertex = getAdjListNode(dest, head[src]);
head[src] = newVertex
}
}####PHP
<?php
class Vertex {
public $label;
function __construct($label) {
$this->label = $label;
}
function getHashcode() {
return $this->label;
}
}
class Graph {
private $adjVertices;
function __construct() {
$this->adjVertices = array();
}
public function addVertex($label) {
if( !in_array($this->adjVertices, $label) ){
$this->adjVertices[$label] = new Vertex($label)
}
}
public function removeVertex($label) {
if( in_array($this->adjVertices, $label)) {
unset($this->adjVertices[$label])
}
}
public function addEdge($label1, $label2) {
$vertex1 = new Vertex($label1)
$vertex2 = new Vertex($label2)
if(in_array($this->adjVertices, $label)) {
$this->adjVertices[$label].append($vertex2)
} else {
$this->adjVertices[$label] = $vertex2
}
}
public function removeEdge($label1, $label2) {
$vertex1 = new Vertex($label1)
$vertex2 = new Vertex($label2)
if(in_array($this->adjVertices, $label1)) {
unset($this->adjVertices[$label])
}
if(in_array($this->adjVertices, $label2)) {
unset($this->adjVertices[$label2])
}
}
public function getTotalVertices() {
return count($adjVertices)
}
}
?>###c) Heaps
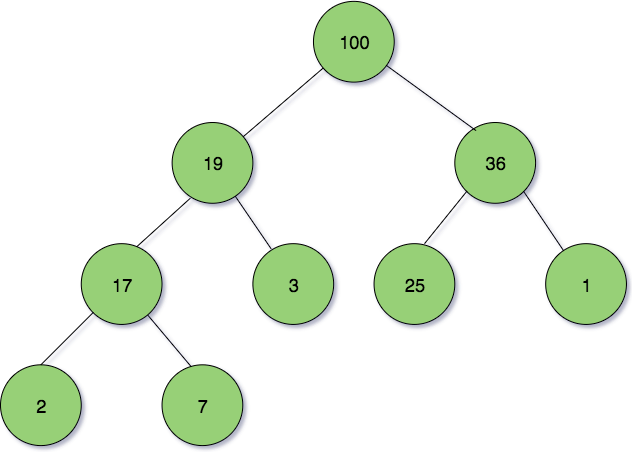
Another data structure that is commonly used. A heap is a special tree-based data structure in which the tree is a complete binary tree. Morever the tree can only be described as a complete as long as it satisfied the heap property condition such as the parent node’s key has an equal value of one of its children node’s key.
They are two main types of heaps here.
Max-Heap: In a max-heap, the key present at the root of the tree must be the greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that same binary tree.
Min-Heap: In a min-heap, the key present at the root of the tree must be the lowest among the keys present at all of its children. The same property must be recursively true for all sub-trees in that same binary tree.
Here are the programming languages’ respective heaps mplementations.
####Java
import java.util.*;
public class Heap {
/** The number of children each node has **/
private static final int d = 2;
private int heapSize;
private int[] heap;
public BinaryHeap(int capacity)
{
heapSize = 0;
heap = new int[capacity + 1];
Arrays.fill(heap, -1);
}
public boolean isEmpty() {
return heapSize == 0;
}
public boolean isFull() {
return heapSize == heap.length;
}
public int parent(int i) {
return (i - 1)/ d;
}
private int kthChild(int i, int k) {
return d * i + k;
}
public void insert(int x) {
if(isFull())
throw new NoSuchElementException("Overflow Exception");
heap[heapSize++] = x;
heapifyUp(heapSize - 1);
}
public int findMin() {
if(isEmpty())
throw new NoSuchElementException("Underflow Exception");
return heap[0]
}
public int deleteMin() {
int keyItem = heap[0];
delete(0);
return keyItem;
}
public int delete(int ind)
{
if (isEmpty() )
throw new NoSuchElementException("Underflow Exception");
int keyItem = heap[ind];
heap[ind] = heap[heapSize - 1];
heapSize--;
heapifyDown(ind);
return keyItem;
}
private void heapifyUp(int childInd)
{
int tmp = heap[childInd];
while (childInd > 0 && tmp < heap[parent(childInd)])
{
heap[childInd] = heap[ parent(childInd) ];
childInd = parent(childInd);
}
heap[childInd] = tmp;
}
private void heapifyDown(int ind)
{
int child;
int tmp = heap[ ind ];
while (kthChild(ind, 1) < heapSize)
{
child = minChild(ind);
if (heap[child] < tmp)
heap[ind] = heap[child];
else
break;
ind = child;
}
heap[ind] = tmp;
}
private int minChild(int ind)
{
int bestChild = kthChild(ind, 1);
int k = 2;
int pos = kthChild(ind, k);
while ((k <= d) && (pos < heapSize))
{
if (heap[pos] < heap[bestChild])
bestChild = pos;
pos = kthChild(ind, k++);
}
return bestChild;
}
}####Python
#!/usr/bin/python
class Heap:
def __init__(self):
self.__heap = []
self.__last_index = -1
def push(self, value):
self.__last_index += 1
if self.__last_index < len(self.__heap):
self.__heap[self.__last_index] = value
else:
self.__heap.append(value)
self.__siftup(self.__last_index)
def pop(self):
if self.__last_index == -1:
raise IndexError('pop from empty heap')
min_value = self.__heap[0]
self.__heap[0] = self.__heap[self.__last_index]
self.__last_index -= 1
self.__siftdown(0)
return min_value
def __siftup(self, index):
while index > 0:
parent_index, parent_value = self.__get_parent(index)
if parent_value <= self.__heap[index]:
break
self.__heap[parent_index], self.__heap[index] =\
self.__heap[index], self.__heap[parent_index]
index = parent_index
def __siftdown(self, index):
while True:
index_value = self.__heap[index]
left_child_index, left_child_value = self.__get_left_child(index, index_value)
right_child_index, right_child_value = self.__get_right_child(index, index_value)
if index_value <= left_child_value and index_value <= right_child_value:
break
if left_child_value < right_child_value:
new_index = left_child_index
else:
new_index = right_child_index
self.__heap[new_index], self.__heap[index] =\
self.__heap[index], self.__heap[new_index]
index = new_index
def __get_parent(self, index):
if index == 0:
return None, None
parent_index = (index - 1) // 2
return parent_index, self.__heap[parent_index]
def __get_left_child(self, index, default_value):
left_child_index = 2 * index + 1
if left_child_index > self.__last_index:
return None, default_value
return left_child_index, self.__heap[left_child_index]
def __get_right_child(self, index, default_value):
right_child_index = 2 * index + 2
if right_child_index > self.__last_index:
return None, default_value
return right_child_index, self.__heap[right_child_index]
def __len__(self):
return self.__last_index + 1
####Ruby
#!/usr/bin/ruby
class Heap
attr_accessor :heap_size, :array_rep
def left_child(index)
2*index + 1
end
def right_child(index)
2*index + 2
end
def left_child_key(index)
@array_rep[left_child(index)]
end
def right_child_key(index)
@array_rep[right_child(index)]
end
end####Javascript
function MinHeap() {
this.data = [];
}
MinHeap.prototype.insert = function(val) {
this.data.push(val);
this.bubbleUp(this.data.length-1);
};
MinHeap.prototype.bubbleUp = function(index) {
while (index > 0) {
// get the parent
var parent = Math.floor((index + 1) / 2) - 1;
// if parent is greater than child
if (this.data[parent] > this.data[index]) {
// swap
var temp = this.data[parent];
this.data[parent] = this.data[index];
this.data[index] = temp;
}
index = parent;
}
};
MinHeap.prototype.extractMin = function() {
var min = this.data[0];
// set first element to last element
this.data[0] = this.data.pop();
// call bubble down
this.bubbleDown(0);
return min;
};
MinHeap.prototype.bubbleDown = function(index) {
while (true) {
var child = (index+1)*2;
var sibling = child - 1;
var toSwap = null;
// if current is greater than child
if (this.data[index] > this.data[child]) {
toSwap = child;
}
// if sibling is smaller than child, but also smaller than current
if (this.data[index] > this.data[sibling] && (this.data[child] == null || (this.data[child] !== null && this.data[sibling] < this.data[child]))) {
toSwap = sibling;
}
// if we don't need to swap, then break.
if (toSwap == null) {
break;
}
var temp = this.data[toSwap];
this.data[toSwap] = this.data[index];
this.data[index] = temp;
index = toSwap;
}
};####C++
// A C++ program to demonstrate common Binary Heap Operations
#include<iostream>
#include<climits>
using namespace std;
// Prototype of a utility function to swap two integers
void swap(int *x, int *y);
// A class for Min Heap
class MinHeap
{
int *harr; // pointer to array of elements in heap
int capacity; // maximum possible size of min heap
int heap_size; // Current number of elements in min heap
public:
// Constructor
MinHeap(int capacity);
// to heapify a subtree with the root at given index
void MinHeapify(int );
int parent(int i) { return (i-1)/2; }
// to get index of left child of node at index i
int left(int i) { return (2*i + 1); }
// to get index of right child of node at index i
int right(int i) { return (2*i + 2); }
// to extract the root which is the minimum element
int extractMin();
// Decreases key value of key at index i to new_val
void decreaseKey(int i, int new_val);
// Returns the minimum key (key at root) from min heap
int getMin() { return harr[0]; }
// Deletes a key stored at index i
void deleteKey(int i);
// Inserts a new key 'k'
void insertKey(int k);
};
// Constructor: Builds a heap from a given array a[] of given size
MinHeap::MinHeap(int cap)
{
heap_size = 0;
capacity = cap;
harr = new int[cap];
}
// Inserts a new key 'k'
void MinHeap::insertKey(int k)
{
if (heap_size == capacity)
{
cout << "\nOverflow: Could not insertKey\n";
return;
}
// First insert the new key at the end
heap_size++;
int i = heap_size - 1;
harr[i] = k;
// Fix the min heap property if it is violated
while (i != 0 && harr[parent(i)] > harr[i])
{
swap(&harr[i], &harr[parent(i)]);
i = parent(i);
}
}
// Decreases value of key at index 'i' to new_val. It is assumed that
// new_val is smaller than harr[i].
void MinHeap::decreaseKey(int i, int new_val)
{
harr[i] = new_val;
while (i != 0 && harr[parent(i)] > harr[i])
{
swap(&harr[i], &harr[parent(i)]);
i = parent(i);
}
}
// Method to remove minimum element (or root) from min heap
int MinHeap::extractMin()
{
if (heap_size <= 0)
return INT_MAX;
if (heap_size == 1)
{
heap_size--;
return harr[0];
}
// Store the minimum value, and remove it from heap
int root = harr[0];
harr[0] = harr[heap_size-1];
heap_size--;
MinHeapify(0);
return root;
}
// This function deletes key at index i. It first reduced value to minus
// infinite, then calls extractMin()
void MinHeap::deleteKey(int i)
{
decreaseKey(i, INT_MIN);
extractMin();
}
// A recursive method to heapify a subtree with the root at given index
// This method assumes that the subtrees are already heapified
void MinHeap::MinHeapify(int i)
{
int l = left(i);
int r = right(i);
int smallest = i;
if (l < heap_size && harr[l] < harr[i])
smallest = l;
if (r < heap_size && harr[r] < harr[smallest])
smallest = r;
if (smallest != i)
{
swap(&harr[i], &harr[smallest]);
MinHeapify(smallest);
}
}
// A utility function to swap two elements
void swap(int *x, int *y)
{
int temp = *x;
*x = *y;
*y = temp;
}
// Driver program to test above functions
int main()
{
MinHeap h(11);
h.insertKey(3);
h.insertKey(2);
h.deleteKey(1);
h.insertKey(15);
h.insertKey(5);
h.insertKey(4);
h.insertKey(45);
cout << h.extractMin() << " ";
cout << h.getMin() << " ";
h.decreaseKey(2, 1);
cout << h.getMin();
return 0;
}####PHP
<?php
class BinaryHeap
{
protected $heap;
public function __construct() {
$this->heap = array();
}
public function isEmpty() {
return empty($this->heap);
}
public function count() {
// returns the heapsize
return count($this->heap) - 1;
}
public function extract() {
if ($this->isEmpty()) {
throw new RunTimeException('Heap is empty');
}
// extract the root item
$root = array_shift($this->heap);
if (!$this->isEmpty()) {
// move last item into the root so the heap is
// no longer disjointed
$last = array_pop($this->heap);
array_unshift($this->heap, $last);
// transform semiheap to heap
$this->adjust(0);
}
return $root;
}
public function compare($item1, $item2) {
if ($item1 === $item2) {
return 0;
}
// reverse the comparison to change to a MinHeap!
return ($item1 > $item2 ? 1 : -1);
}
protected function isLeaf($node) {
// there will always be 2n + 1 nodes in the
// sub-heap
return ((2 * $node) + 1) > $this->count();
}
protected function adjust($root) {
// we've gone as far as we can down the tree if
// root is a leaf
if (!$this->isLeaf($root)) {
$left = (2 * $root) + 1; // left child
$right = (2 * $root) + 2; // right child
// if root is less than either of its children
$h = $this->heap;
if (
(isset($h[$left]) &&
$this->compare($h[$root], $h[$left]) < 0)
|| (isset($h[$right]) &&
$this->compare($h[$root], $h[$right]) < 0)
) {
// find the larger child
if (isset($h[$left]) && isset($h[$right])) {
$j = ($this->compare($h[$left], $h[$right]) >= 0)
? $left : $right;
}
else if (isset($h[$left])) {
$j = $left; // left child only
}
else {
$j = $right; // right child only
}
// swap places with root
list($this->heap[$root], $this->heap[$j]) =
array($this->heap[$j], $this->heap[$root]);
// recursively adjust semiheap rooted at new
// node j
$this->adjust($j);
}
}
}
}###d) Trie
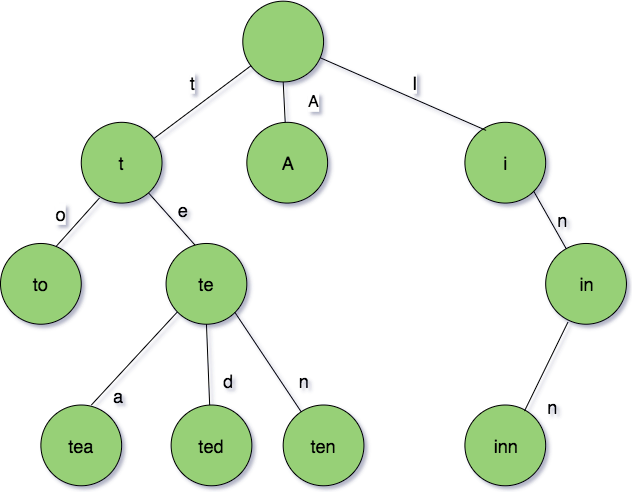
In computer science, a trie is an ordered search tree that is used to store a dynamic set or associative array where the keys are usually strings. Like an ordered search tree or graph, trie is designed to determine the most efficient way of traversing and retrieving of data by mainly relying on the string prefixes.
It consists of nodes and edges much like graphs and trees. Each node consists of max 26 children and edges connect each parent node to its children. These 26 pointers are nothing but pointers for each of the 26 letters of English alphabet. A separate edge is maintained for every edge.
String are stored in a top to bottom fashion manner on the basis of their prefix in a trie. All prefixes of length 1 are stored at until level 1, all prefixes of length of 2 are stored at until level 2 and so on.
Again, here are the languages’ queue implementations.
####Java
import java.util.Arrays;
public class Trie {
static final int ALPHABET_SIZE = 26;
static class TrieNode {
TrieNode[] children = new TrieNode[ALPHABET_SIZE];
boolean isEndOfWord;
TrieNode() {
isEndOfWord = false;
for(int i =0; i < ALPHABET_SIZE; i++)
children[i] = null;
}
}
static TrieNode root;
static void insert(String key) {
int level;
int length = key.length();
int index;
TrieNode pCrawl = root;
for(level = 0; level < length; level++) {
index = key.charAt(level) - 'a';
if(pCrawl.children[index] == null)
pCrawl.children[index] = new TrieNode();
pCrawl = pCrawl.children[index];
}
pCrawl.isEndOfWord = true;
}
static boolean search(String key) {
int level;
int length = key.length();
int index;
TrieNode pCrawl = root;
for(level = 0; level < length; level++) {
index = key.charAt(level) - 'a';
if(pCrawl.children[index] == null)
return false;
pCrawl = pCrawl.children[index];
}
return (pCrawl != null && pCrawl.isEndOfWord);
}
}####Python
#!/usr/bin/python
from typing import Tuple
class TrieNode(object):
"""
Our trie node implementation. Very basic. but does the job
"""
def __init__(self, char: str):
self.char = char
self.children = []
# Is it the last character of the word.`
self.word_finished = False
# How many times this character appeared in the addition process
self.counter = 1
def add(root, word: str):
"""
Adding a word in the trie structure
"""
node = root
for char in word:
found_in_child = False
# Search for the character in the children of the present `node`
for child in node.children:
if child.char == char:
# We found it, increase the counter by 1 to keep track that another
# word has it as well
child.counter += 1
# And point the node to the child that contains this char
node = child
found_in_child = True
break
# We did not find it so add a new chlid
if not found_in_child:
new_node = TrieNode(char)
node.children.append(new_node)
# And then point node to the new child
node = new_node
# Everything finished. Mark it as the end of a word.
node.word_finished = True
def find_prefix(root, prefix: str) -> Tuple[bool, int]:
"""
Check and return
1. If the prefix exsists in any of the words we added so far
2. If yes then how may words actually have the prefix
"""
node = root
# If the root node has no children, then return False.
# Because it means we are trying to search in an empty trie
if not root.children:
return False, 0
for char in prefix:
char_not_found = True
# Search through all the children of the present `node`
for child in node.children:
if child.char == char:
# We found the char existing in the child.
char_not_found = False
# Assign node as the child containing the char and break
node = child
break
# Return False anyway when we did not find a char.
if char_not_found:
return False, 0
# Well, we are here means we have found the prefix. Return true to indicate that
# And also the counter of the last node. This indicates how many words have this
# prefix
return True, node.counter
if __name__ == "__main__":
root = TrieNode('*')
add(root, "hackathon")
add(root, 'hack')
####Ruby
#!/usr/bin/ruby
class Node
attr_reader :data, :children
attr_accessor :term
def initialize(data)
@data = data
@children = []
@term = false
end
def insert(char)
return get(char) if have?(char)
child = Node.new(char)
@children << child
child
end
def have?(char)
@children.each do |c|
return true if c.data == char
end
false
end
def get(char)
@children.each do |child|
return child if child.data == char
end
false
end
end
class Trie
attr_reader :root
def initialize
@root = Node.new(nil)
end
def insert(word)
node = @root
word.size.times do |i|
child = node.insert(word[i])
node = child
end
node.term = true
end
def have?(word)
node = @root
word.size.times do |i|
return false unless node.have?(word[i])
node = node.get(word[i])
end
return node.term == true
end
end####Javascript
function Trie() {
this.head = {
key : ''
, children: {}
}
}
Trie.prototype.add = function(key) {
var curNode = this.head
, newNode = null
, curChar = key.slice(0,1);
key = key.slice(1);
while(typeof curNode.children[curChar] !== "undefined"
&& curChar.length > 0){
curNode = curNode.children[curChar];
curChar = key.slice(0,1);
key = key.slice(1);
}
while(curChar.length > 0) {
newNode = {
key : curChar
, value : key.length === 0 ? null : undefined
, children : {}
};
curNode.children[curChar] = newNode;
curNode = newNode;
curChar = key.slice(0,1);
key = key.slice(1);
}
};
Trie.prototype.search = function(key) {
var curNode = this.head
, curChar = key.slice(0,1)
, d = 0;
key = key.slice(1);
while(typeof curNode.children[curChar] !== "undefined" && curChar.length > 0){
curNode = curNode.children[curChar];
curChar = key.slice(0,1);
key = key.slice(1);
d += 1;
}
if (curNode.value === null && key.length === 0) {
return d;
} else {
return -1;
}
}
Trie.prototype.remove = function(key) {
var d = this.search(key);
if (d > -1){
removeH(this.head, key, d);
}
}
function removeH(node, key, depth) {
if (depth === 0 && Object.keys(node.children).length === 0){
return true;
}
var curChar = key.slice(0,1);
if (removeH(node.children[curChar], key.slice(1), depth-1)) {
delete node.children[curChar];
if (Object.keys(node.children).length === 0) {
return true;
} else {
return false;
}
} else {
return false;
}
}
####C++
#include <iostream>
// define character size
#define CHAR_SIZE 128
// A Class representing a Trie node
class Trie
{
public:
bool isLeaf;
Trie* character[CHAR_SIZE];
// Constructor
Trie()
{
this->isLeaf = false;
for (int i = 0; i < CHAR_SIZE; i++)
this->character[i] = nullptr;
}
void insert(std::string);
bool deletion(Trie*&, std::string);
bool search(std::string);
bool haveChildren(Trie const*);
};
// Iterative function to insert a key in the Trie
void Trie::insert(std::string key)
{
// start from root node
Trie* curr = this;
for (int i = 0; i < key.length(); i++)
{
// create a new node if path doesn't exists
if (curr->character[key[i]] == nullptr)
curr->character[key[i]] = new Trie();
// go to next node
curr = curr->character[key[i]];
}
// mark current node as leaf
curr->isLeaf = true;
}
// Iterative function to search a key in Trie. It returns true
// if the key is found in the Trie, else it returns false
bool Trie::search(std::string key)
{
// return false if Trie is empty
if (this == nullptr)
return false;
Trie* curr = this;
for (int i = 0; i < key.length(); i++)
{
// go to next node
curr = curr->character[key[i]];
// if string is invalid (reached end of path in Trie)
if (curr == nullptr)
return false;
}
// if current node is a leaf and we have reached the
// end of the string, return true
return curr->isLeaf;
}
// returns true if given node has any children
bool Trie::haveChildren(Trie const* curr)
{
for (int i = 0; i < CHAR_SIZE; i++)
if (curr->character[i])
return true; // child found
return false;
}
// Recursive function to delete a key in the Trie
bool Trie::deletion(Trie*& curr, std::string key)
{
// return if Trie is empty
if (curr == nullptr)
return false;
// if we have not reached the end of the key
if (key.length())
{
// recurse for the node corresponding to next character in the key
// and if it returns true, delete current node (if it is non-leaf)
if (curr != nullptr &&
curr->character[key[0]] != nullptr &&
deletion(curr->character[key[0]], key.substr(1)) &&
curr->isLeaf == false)
{
if (!haveChildren(curr))
{
delete curr;
curr = nullptr;
return true;
}
else {
return false;
}
}
}
// if we have reached the end of the key
if (key.length() == 0 && curr->isLeaf)
{
// if current node is a leaf node and don't have any children
if (!haveChildren(curr))
{
// delete current node
delete curr;
curr = nullptr;
// delete non-leaf parent nodes
return true;
}
// if current node is a leaf node and have children
else
{
// mark current node as non-leaf node (DON'T DELETE IT)
curr->isLeaf = false;
// don't delete its parent nodes
return false;
}
}
return false;
}
// C++ implementation of Trie Data Structure
int main()
{
Trie* head = new Trie();
head->insert("hello");
std::cout << head->search("hello") << " "; // print 1
head->insert("helloworld");
std::cout << head->search("helloworld") << " "; // print 1
std::cout << head->search("helll") << " "; // print 0 (Not found)
head->insert("hell");
std::cout << head->search("hell") << " "; // print 1
head->insert("h");
std::cout << head->search("h"); // print 1
std::cout << std::endl;
head->deletion(head, "hello");
std::cout << head->search("hello") << " "; // print 0
std::cout << head->search("helloworld") << " "; // print 1
std::cout << head->search("hell"); // print 1
std::cout << std::endl;
head->deletion(head, "h");
std::cout << head->search("h") << " "; // print 0
std::cout << head->search("hell") << " "; // print 1
std::cout << head->search("helloworld"); // print 1
std::cout << std::endl;
head->deletion(head, "helloworld");
std::cout << head->search("helloworld") << " "; // print 0
std::cout << head->search("hell") << " "; // print 1
head->deletion(head, "hell");
std::cout << head->search("hell"); // print 0
std::cout << std::endl;
if (head == nullptr)
std::cout << "Trie empty!!\n"; // Trie is empty now
std::cout << head->search("hell"); // print 0
return 0;
}####PHP
<?php
class TrieNode {
public $weight;
private $children;
function __construct($weight, $children) {
$this->weight = $weight;
$this->children = $children;
}
/** map lower case english letters to 0-25 */
static function getAsciiValue($char) {
return intval(ord($char)) - intval(ord('a'));
}
function addChild($char, $node) {
if (!isset($this->children)) {
$this->children = [];
}
$this->children[self::getAsciiValue($char)] = $node;
}
function isChild($char) {
return isset($this->children[self::getAsciiValue($char)]);
}
function getChild($char) {
return $this->children[self::getAsciiValue($char)];
}
function isLeaf() {
return empty($this->children);
}
}That’s all for common linear-type data structures.
And that’s the end of knowing-your-algorithms-and-data-structures series in my blog post.
Hope you learn something useful out of them.
Till then. Happy Coding!